Tracking error
In finance, tracking error is a measure of how closely a portfolio follows the index to which it is benchmarked. The most common measure is the root-mean-square of the difference between the portfolio and index returns.
Many portfolios are managed to a benchmark, normally an index. Some portfolios are expected to replicate, before trading and other costs, the returns of an index exactly (an index fund), while others are expected to 'actively manage' the portfolio by deviating slightly from the index in order to generate active returns or to lower transaction costs. Tracking error (also called active risk) is a measure of the deviation from the benchmark; the aforementioned index fund would have a tracking error close to zero, while an actively managed portfolio would normally have a higher tracking error. Dividing portfolio active return by portfolio tracking error gives the information ratio, which is a risk adjusted performance metric.
Contents |
Definition
If tracking error is measured historically, it is called 'realised' or 'ex post' tracking error. If a model is used to predict tracking error, it is called 'ex ante' tracking error. The former is more useful for reporting performance, whereas ex ante is generally used by portfolio managers to control risk. Various types of ex-ante tracking error models exist, from simple equity models which use beta as a primary determinant to more complicated multi-factor fixed income models.
Formulas
The ex-post Tracking Error formula is the deviation of the active returns,[1] given by:
![T.E. = \omega =\sqrt{\operatorname{E}[(d - b)^2]}](/2012-wikipedia_en_all_nopic_01_2012/I/a7e2a2f99982309d4bb50ed9f48fd680.png)
Nevertheless it is commonly calculated as Standard deviation of returns relative to benchmark:
![T.E. = \omega =\sqrt{\operatorname{Var}(d - b)} = \sqrt{{E}[(d-b)^2]-({E}[d - b])^2}](/2012-wikipedia_en_all_nopic_01_2012/I/318129027dcce17a8f3244cdf0ff0ea6.png)
which in case of large portfolio deviations would lessen TE significantly and mislead its original meaning. This volatility definition makes sense, however, if the tracking error is to be used in an information ratio.
where 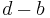 is the difference between the portfolio return and the index return for period i and N is the number of observations
is the difference between the portfolio return and the index return for period i and N is the number of observations
Examples
- Index funds are expected to have minimal tracking errors.
- Inverse exchange-traded funds are designed to perform as the inverse of an index or other benchmark, and thus reflect tracking errors relative to short positions in the underlying index or benchmark.
References
- ^ Grinold, R. and Kahn, R., "Active Portfolio Management", McGraw-Hill, 1999